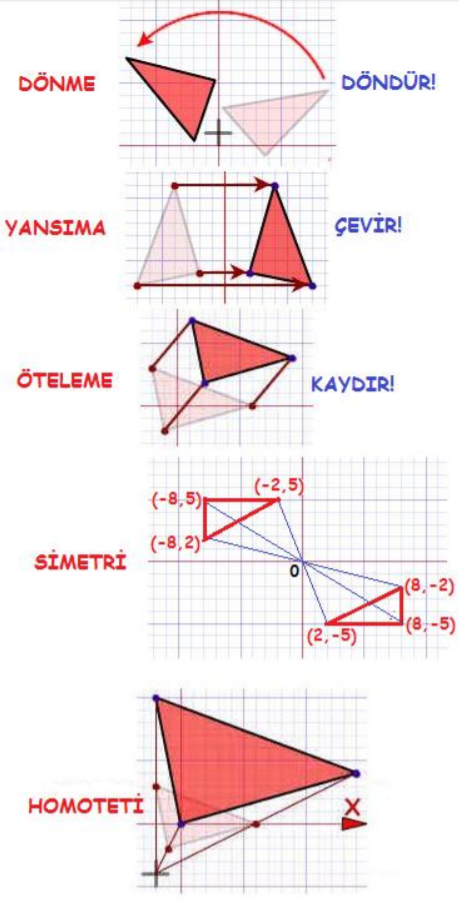
1. ANALİTİK DÜZLEMDE SİMETRİ
Noktaya göre simetrik şekillerin karşılıklı noktaları;
Simetri Merkezinden eşit uzaklıktadır,
Simetri merkezinin ters yönündedir.
Analitik düzlemde;
P(x,y) noktasının, O(0,0) başlangıç noktasına göre simetriği P’(-x, -y) dir.
P(x,y) noktasının, A(a,b) noktasına göre simetriği P’(2a-x, 2b-y) dir.
2. YANSIMA

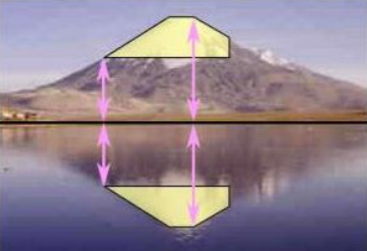
Doğruya göre simetrik şekillerin karşılıklı noktaları;
Simetri Ekseninden eşit uzaklıktadır,
Şeklin boyutu değişmez.
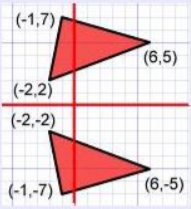
Analitik düzlemde P(x,y) noktasının;
0x eksenine göre simetriği P1(x, -y)
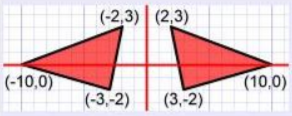
0y eksenine göre simetriği P2(-x, y)
y=x doğrusuna göre simetriği P3(y, x)
y=-x doğrusuna göre simetriği P4(-y, -x)
3. DÖNME
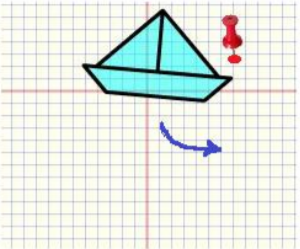
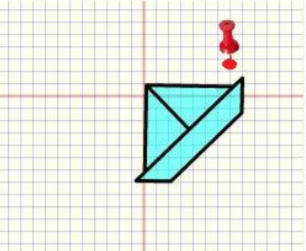
Döndürülecek şeklin tüm noktaları, Dönme merkezi etrafında eşit açılar çizecek şekilde döndürülür. Noktaya göre simetri, 180° lik dönmeye karşı gelir.
Analitik düzlemde;
P(x, y) noktasının, O(0,0) Başlangıç noktası etrafında 90° lik (Pozitif yönde) dönmesine karşı gelen nokta P’(-y, x) dir.
4. ÖTELEME
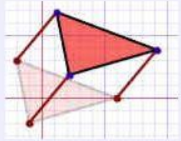
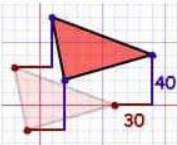
Ötelenen şeklin tüm noktaları, aynı doğrultuda ve aynı uzaklıkta ötelenir.
Analitik düzlemde P(x,y) noktası;
0x ekseni doğrultusunda a birim ötelendiğinde P1(x+a, y)
0y ekseni doğrultusunda b birim ötelendiğinde P2(x, y+b)
Her iki işlem birlikte yapıldığında P3(x+a, y+b) olur.
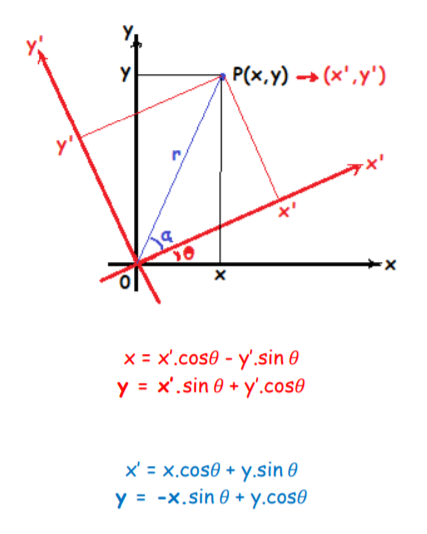
5. KOORDİNATLARIN DÖNÜŞÜMÜ
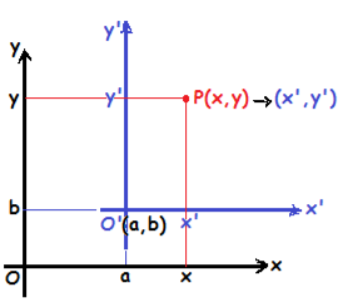
0xy dik koordinat sistemi, eksenler paralel kalacak şekilde 0(0,0) başlangıç noktası 0’(a,b) noktasına kaydırılır.
0xy sisteminde P(x,y) noktası, 0’x’y’ koordinat sisteminde P(x’,y’) olarak gösterilir.
x = x’+a , y = y’+b
x’ = x - a , y’ = y - b
6. EKSENLERİN DÖNDÜRÜLMESİ